Exponential Function Increasing Or Decreasing

Exponential Role

The exponential part is a blazon of mathematical part which are helpful in finding the growth or disuse of population, coin, toll, etc that are growing or decay exponentially. Jonathan was reading a news article on the latest research made on bacterial growth. He read that an experiment was conducted with ane bacterium. Later the start 60 minutes, the bacterium doubled itself and was two in number. Afterwards the second hour, the number was iv. At every hour the number of leaner was increasing. He was thinking what would be the number of leaner after 100 hours if this blueprint continues. When he asked his instructor about the same the answer he got was the concept of an exponential function.

Allow us acquire more nigh exponential function along with its definition, equation, graphs, exponential growth, exponential decay, etc.

1.	What is Exponential Function?
2.	Exponential Role Formula
3.	Exponential Function Graph
4.	Exponential Function Asymptotes
5.	Domain and Range of Exponential Function
6.	Exponential Serial
vii.	Exponential Function Rules
viii.	Derivative of Exponential Function
9.	Integration of Exponential Office
10.	FAQs on Exponential Function

What is Exponential Function?

Exponential function, as its name suggests, involves exponents. But annotation that, an exponential function has a abiding as its base and a variable equally its exponent just not the other way circular (if a function has a variable as the base and a constant as the exponent then it is a power function but not an exponential office). An exponential function tin be in 1 of the following forms.

Exponential Office Definition

In mathematics, an exponential function is a function of form f (10) = a^x, where "10" is a variable and "a" is a constant which is chosen the base of the role and information technology should be greater than 0.

Exponential Function Examples

Hither are some examples of exponential office.

• f(x) = 2^x
• f(x) = (i/2)¹⁰
• f(x) = 3e^2x
• f(x) = 4 (3)^-0.5x

Exponential Office Formula

A basic exponential function, from its definition, is of the course f(x) = b^x, where 'b' is a constant and 'ten' is a variable. One of the pop exponential functions is f(x) = e^x, where 'e' is "Euler's number" and e = 2.718....If we extend the possibilities of different exponential functions, an exponential role may involve a constant as a multiple of the variable in its power. i.east., an exponential role tin likewise be of the course f(x) = e^kx. Farther, information technology can also be of the form f(x) = p eastward^kx, where 'p' is a constant. Thus, an exponential function tin can be in 1 of the post-obit forms.

• f(10) = b^x
• f(x) = ab^x
• f(x) = ab^cx
• f(x) = e¹⁰
• f(x) = e^kx
• f(10) = p e^kx

Here, apart from 'x' all other letters are constants, 'x' is a variable, and f(ten) is an exponential office in terms of ten. Also, note that the base in each exponential function must be a positive number. i.eastward., in the in a higher place functions, b > 0 and due east > 0. Likewise, b should non be equal to 1 (if b = 1, and so the function f(10) = b¹⁰ becomes f(ten) = 1 and in this instance, the function is linear but Non exponential).

The exponential function arises whenever a quantity's value increases in exponential growth and decreases in exponential decay. We tin see more differences between exponential growth and disuse along with their formulas in the post-obit table.

Exponential Growth	Exponential Disuse
In exponential growth, a quantity slowly increases in the first and then it increases chop-chop.	In exponential decay, a quantity decreases very speedily in the offset, and and then information technology decreases slowly.
The exponential growth formulas are used to model population growth, to model compound involvement, to find doubling time, etc	The exponential disuse is helpful to model population decay, to find half-life, etc.
The graph of the function in exponential growth is increasing.	The graph of the role in exponential growth is decreasing.
In exponential growth, the office can be of the class: f(x) = abx, where b > 1. f(x) = a (1 + r)x P = P0 eyard t Here, b = 1 + r ≈ eone thousand.	In exponential decay, the function can be of the form: f(10) = abx, where 0 < b < i. f(10) = a (1 - r)10 P = P0 due east-one thousand t Here, b = i - r ≈ eastward- chiliad.

In the above formulas,

• a (or) P₀ = Initial value
• r = Rate of growth
• 1000 = abiding of proportionality
• x (or) t = time (fourth dimension tin can be in years, days, (or) months. Whatever we are using should be consequent throughout the problem).

Exponential Function Graph

We tin understand the process of graphing exponential role by taking some examples. Let us graph two functions f(10) = 2^x and chiliad(10) = (1/2)^x. To graph each of these functions, nosotros volition construct a table of values with some random values of 10, plot the points on the graph, connect them past a curve, and extend the curve on both ends. The procedure of graphing exponential part can be learned in detail by clicking here.

Here is the table of values that are used to graph the exponential part f(10) = 2¹⁰.

Hither is the table of values that are used to graph the exponential function g(x) = (1/2)^x.

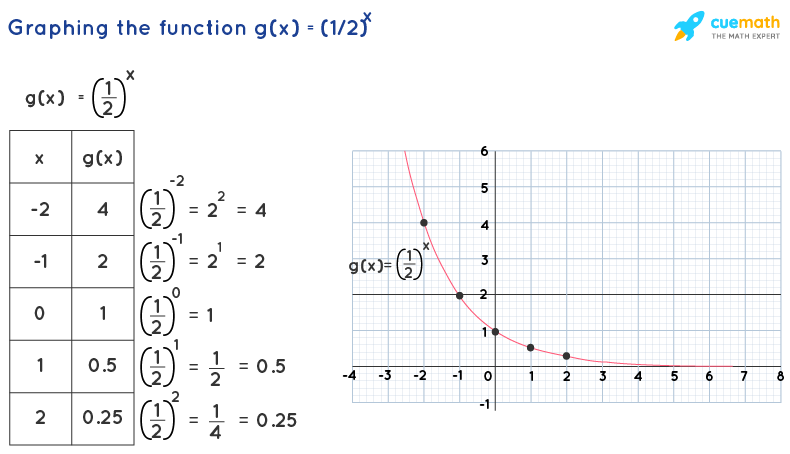
Annotation: From the in a higher place two graphs, nosotros tin encounter that f(x) = ii¹⁰ is increasing whereas thousand(ten) = (1/2)^x is decreasing. Thus, the graph of exponential function f(x) = b^ten.

• increases when b > i
• decreases when 0 < b < 1

Exponential Role Asymptotes

The exponential office has no vertical asymptote as the part is continuously increasing/decreasing. Only it has a horizontal asymptote. The equation of horizontal asymptote of an exponential funtion f(x) = ab^x + c is ever y = c. i.e., it is nothing but "y = constant being added to the exponent part of the function". In the above ii graphs (of f(10) = 2^x and g(10) = (one/2)¹⁰), we can notice that the horizontal asymptote is y = 0 as zero is being added to the exponent role in both the functions. Thus,

• An exponential function never has a vertical asymptote.
• The horizontal asymptote of an exponential office f(10) = ab^x + c is y = c.

Domain and Range of Exponential Office

We know that the domain of a part y = f(x) is the set of all x-values (inputs) where it tin be computed and the range is the gear up of all y-values (outputs) of the function. From the graphs of f(x) = ii^x and yard(x) = (1/2)^x in the previous section, we tin see that an exponential part can be computed at all values of ten. Thus, the domain of an exponential function is the set of all real numbers (or) (-∞, ∞). The range of an exponential function can exist determined by the horizontal asymptote of the graph, say, y = d, and by seeing whether the graph is above y = d or below y = d. Thus, for an exponential office f(x) = ab^x,

• Domain is the set of all real numbers (or) (-∞, ∞).
• Range is f(x) > d if a > 0 and f(x) < d if a < 0.

To understand this, y'all can see the example beneath.

Exponential Series

The real exponential part tin can be commonly defined by the following power series,

east^ten = Σ_{n = 0} ^∞  xⁿ/northward! = i + (10/one) + (ten²/two) + (x^three/6) + ...

Expansion of some other exponential functions are given as shown below,

e = Σ_{northward = 0} ^∞ oneⁿ/north! = 1 + (1/1) + (i/2) + (1/6) + ...

eastward^-1 = Σ_{n = 0} ^∞ (-1)^{due north}/due north! = ane - (i/one) + (one/ii) - (1/half dozen) + ...

Exponential Part Rules

The rules of exponential function are every bit aforementioned equally that of rules of exponents. Here are some rules of exponents.

• Law of Null Exponent: a⁰ = 1
• Law of Product: a^m × a^{due north} = a^m+northward
• Law of Quotient: a^m/aⁿ = a^{m-due north}
• Law of Power of a Ability: (a^m)ⁿ = a^mn
• Law of Power of a Production: (ab)^k = a^mb^m
• Law of Power of a Caliber: (a/b)^m = a^grand/b^grand
• Law of Negative Exponent: a^-m = one/a^m

Apart from these, we sometimes need to use the conversion formula of logarithmic class to exponential form which is:

• b^x = a ⇔ log_b a = x

Equality Property of Exponential Role

According to the equality property of exponential function, if 2 exponential functions of the same bases are the same, then their exponents are as well the same. i.due east.,

b^x₁ = b^x₂ ⇔ 10₁ = x₂

Exponential Function Derivative

Here are the formulas from differentiation that are used to find the derivative of exponential function.

• d/dx (e^x) = e^ten
• d/dx (a¹⁰) = a^x · ln a.

Integration of Exponential Role

Here are the formulas from integration that are used to find the integral of exponential function.

• ∫ east¹⁰ dx = eastward^ten + C
• ∫ a¹⁰ dx = a^x / (ln a) + C

Important Notes on Exponential Part:

• The domain of any exponential function is the set of all existent numbers.
• An exponential function has no vertical asymptote.
• Every exponential function has one horizontal asymptote.
• The graph of any exponential office is either increasing or decreasing.

☛ Related Topics:

• Exponential Function Calculator
• Logarithmic Functions
• Exponential Equations

Examples on Exponential Role

1. Example i: In 2010, in that location were 100,000 citizens in a boondocks. If the population increases by viii% every year, then how many citizens volition there exist in 10 years? Round your answer to the nearest integer.

   Solution:

   The initial population is, a = 100,000.

   The rate of growth is, r = 8% = 0.08.

   The time is, x = x years.

   Using the exponential growth formula,

   f(x) = a (1 + r)^x

   f(10) = 100000(one + 0.08)¹⁰

   f(x) ≈ 215,892 (rounded to the nearest integer)

   Answer: Therefore, the number of citizens in 10 years will be 215,892.

2. Example 2: The half-life of carbon-xiv is 5,730 years. If in that location were chiliad grams of carbon initially, then what is the amount of carbon left after 2000 years? Round your answer to the nearest integer.

   Solution:

   Using the given data, nosotros can say that carbon-14 is decaying and hence we use the formula of exponential decay.

   P = P₀ e^{- k t} ... (1),

   Here, P₀ = initial amount of carbon = 1000 grams.

   It is given that the half-life of carbon-fourteen is v,730 years. It means

   P = P₀ / 2 = 1000 / two = 500 grams.

   Substitute all these values in (1),

   500 = yard eastward^{- k (5730)}

   Dividing both sides past m,

   0.5 = e^{- yard (5730)}

   Taking "ln" on both sides,

   ln 0.five = -5730k

   Dividing both sides by -5730,

   m = ln 0.five / (-5730) ≈ 0.00012097

   We have to find the amount of carbon that is left after 2000 years. Substitute t = 2000 in (1),

   P = k e^{- (0.00012097) (2000)} ≈ 785 grams.

   Answer: The amount of carbon left afterward yard years = 785 grams.

3. Example 3: Simplify the following exponential expression: iii^x - iii^x+two

   Solution:

   Given exponential equation: 3^x - 3^ten+2

   By using the property: a^x a^y = a^x+y

   Hence, 3^x+ii can exist written as 3^x.3²

   Thus the given equation is written every bit:

   3^ten - 3¹⁰⁺² = iii^x - iii^x·9

   At present, cistron out the term 3¹⁰

   three^x - 3^x+two = 3^x - 3^x·9 = 3¹⁰(1 - 9)

   three^x - three^x+2 = 3^x(-8)

   3^ten - 3¹⁰⁺ⁱⁱ = -eight(iii^ten)

   Answer:Therefore, the simplification of the given expoential equation 3^x-3^10+ane is -8(3^x).

become to slidego to slidego to slide

Bang-up learning in loftier school using simple cues

Indulging in rote learning, you lot are likely to forget concepts. With Cuemath, you volition larn visually and exist surprised by the outcomes.

Book a Free Trial Class

Practice Questions on Exponential Functions

go to slidego to slidego to slide

FAQs on Exponential Function

What is the Definition of Exponential Function?

An exponential function is a type of part in math that involves exponents. A bones exponential office is of the class f(x) = b^x, where b > 0 and b ≠ one.

What are the Formulas of Exponential Function?

The formulas of an exponential function accept exponents in them. An exponential equation can be in one of the post-obit forms.

• f(ten) = ab^cx
• f(x) = p due east^kx

What are the Rules of Exponential Function?

Since the exponential function involves exponents, the rules of exponential function are as same as the rules of exponents. They are:

• a^thousand × a^north = a^m+northward
• a^k/a^northward = a^m-n
• a⁰ = one
• a^-m = i/a^grand
• (a^m)^north = a^mn
• (ab)^m = a^mb^m
• (a/b)^thousand = a^m/b^m

How to Graph Exponential Function?

To graph an exponential function y = f(ten), create a table of values by taking some random numbers for ten (commonly we take -2, -i, 0, 1, and 2), and substitute each of them in the office to find the respective y values. Then plot the points from the tabular array and join them past a curve. Finally, extend the curve on both ends. Keep a annotation of horizontal asymptote while drawing the graph.

What is the Domain of Exponential Function?

An exponential function f(x) = ab^x is defined for all values of x and hence its domain is the ready of all existent numbers, which in interval notation tin exist written as (-∞, ∞).

What are the Properties of Exponential Function?

The properties of exponential function tin be given as,

• a^m × aⁿ = a^m+n
• a^m/aⁿ = a^thousand-n
• a⁰ = 1
• a^-m = 1/a^m
• (a^m)ⁿ = a^mn
• (ab)^g = a^thousandb^m
• (a/b)^{one thousand} = a^chiliad/b^thou

For any exponential function of the course f(x) = ab^x, where b > 1, the exponential graph increases while for any exponential office of the form f(x) = ab¹⁰, where 0 < b < 1, the graph decreases.

What is the Range of Exponential Function?

The range of an exponential office depends upon its horizontal asymptote and as well whether the curve lies above or beneath the horizontal asymptote. i.e., for an exponential function f(x) = ab¹⁰, the range is

• f(ten) > d if a > 0 and
• f(x) < d if a < 0,

where y = d is the horizontal asymptote of the graph of the part.

What is the Equality Property of Exponential Role?

The equality belongings of exponential role says if two values (outputs) of an exponential function are equal, then the respective inputs are also equal. i.eastward., b^x₁ = b^x₂ ⇔ 10₁ = x₂.

What is the Derivative of Exponential Part?

An exponential function may be of the grade e^x or a^x. The formulas to find the derivatives of these functions are as follows:

• The derivative of eastward^x is, d/dx (e^ten) = east^x
• d/dx (a^x) = a^x · ln a.

What is the Integral of Exponential Function?

An exponential function may be of the form due east^x or a^ten. The formulas to find the integrals of these functions are equally follows:

• The integral of e^x is, ∫ e^x dx = east^ten + C
• ∫ a¹⁰ dx = a^x / (ln a) + C

Exponential Function Increasing Or Decreasing,

Source: https://www.cuemath.com/calculus/exponential-functions/

Posted by: moratrailtandes.blogspot.com

Share this post